工业领域中，许多工艺过程都涉及液相对固相的润湿过程，比如涂料行业里的固液混合及分散，喷涂行业里的固体表面涂覆，食品加工业里的固体材料的浸渍等等。这些润湿步骤对成品的质量起到关键性的作用。

真空润湿性，是指材料在接近绝对真空的条件下，其固态表面可被润湿的程度。在接近真空的环境下，原本夹带空气的聚集颗粒，可以被更好地分散成单个一次颗粒，从而增大其润湿接触面，提高其润湿性。比如在高真空度下，分散并润湿二氧化硅颗粒。

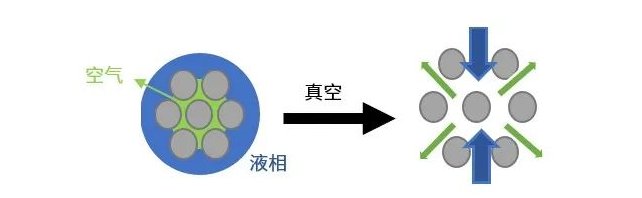
图1.颗粒聚集体的真空润湿

另外在锂电行业，提高真空度，可以排出气泡，让电解液倒吸至多孔电极表面，并更好地润湿电极。而在毛细管流孔径分析过程中，也需要先准备一个真空环境，并在此环境下让润湿液流过孔道。所以，固体材料的真空可润湿性也是一个重要的物理性质。

一般我们将真空下的可润湿性记作：

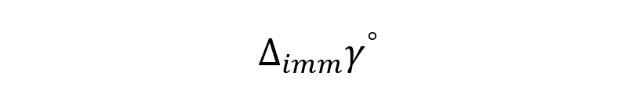
其定义如下：

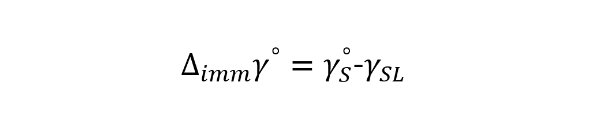
上式中，γos 为固体在真空下的表面张力（也称表面能），γSL 为被润湿后的固体表面张力。△immγo也可以称为真空润湿功，其负值为真空润湿过程的吉布斯（Gibbs）自由能，即:

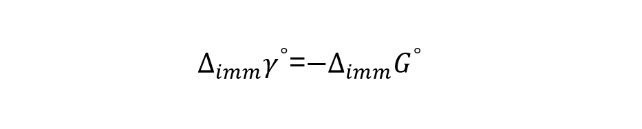
其实我们通过气体物理吸附等温线，结合 Gibbs 吸附等温线，可以理论计算出固体材料的真空润湿功。Gibbs 吸附等温式如下：

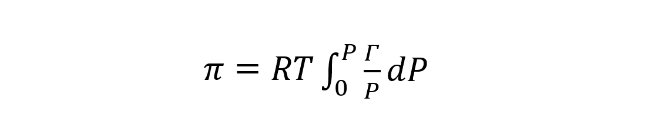
上式中，π 为吸附质在吸附剂表面的扩展压，其为吸附前后，固体表面张力值的变化：π = γos-γSG。Γ 为表面剩余浓度，在常压范围内的吸附过程中，Γ=na/A，na 为累计吸附量，A 为固体的表面积，P 为吸附绝对压力。

我们选取了两种负载金属的催化剂和一种锂电负极碳材料进行了计算。它们的吸附等温线都是典型的 II 型等温线，可以用 BET 吸附等温线描述。见下图：

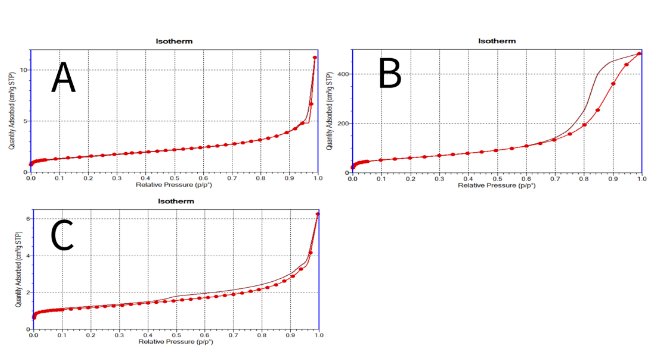
图2.两种催化剂（A与B）和碳负极材料C的等温吸附线，催化剂B含有介孔结构

催化剂 A 和负极材料 C 使用了 ASAP 2460 测试，含介孔的催化剂 B 使用了 Tristar II plus 3030 测试，皆为 77K 下的氮气吸附。

 Micromeritics Tristar II plus 物理吸附仪 

结合BET吸附等温式，我们可以得到：

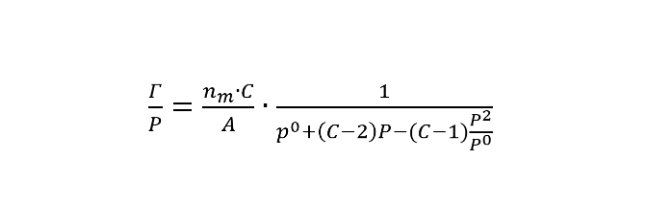
P0 为 77K 下液氮的饱和蒸汽压：760 mmHg，nm 为单位质量 BET 单层饱和吸附量，C 为 BET 方程常数，A 为材料的 BET 比表面积。这里的这些参数皆可以由麦克分析软件中的 Autofit 分析报告给出。当确定上式右边的形式后，在进行吸附压力 0 至 760 mmHg 的积分，便可求出 π（P0）。

图3. Autofit报告及相关参数

当对材料 A 计算值时，可见随着吸附压力上升，π 值增大，说明随着氮气的吸附，材料的表面能不断降低。

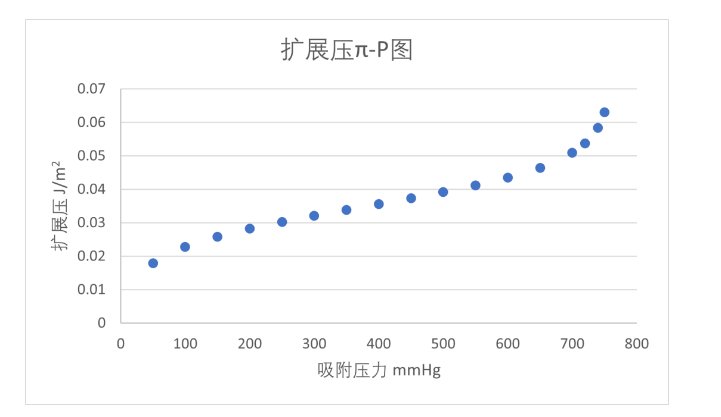
图4. 催化剂A的扩展压-吸附压图

由于 BET 方程的特性，积分项在 P=760 mmHg 处会发散，故取压力接近 760 mmHg 的值作为积分上限。发现随着压力接近 760 mmHg，值趋于固定。

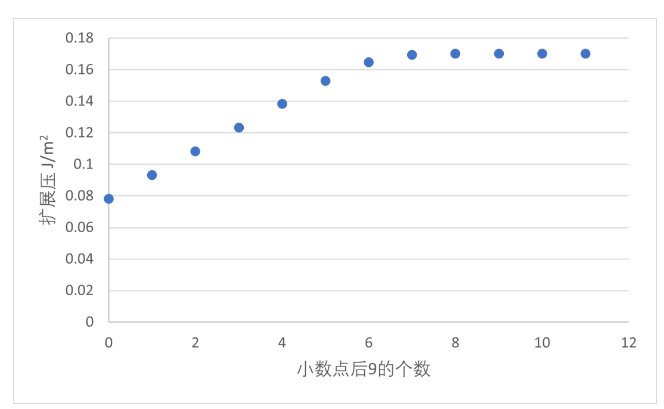
图5. 催化剂 A 的 π 值随着压力接近 760 mmHg 的变化

采用同样的办法，也可以计算出催化剂 B 和碳材料 C 的扩展压。需结合 Young 氏方程：

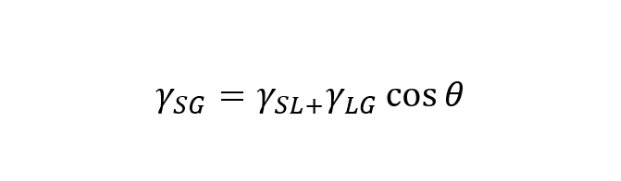
上式中，γ 为在气相平衡下的润湿液体的表面张力，θ 为接触角。我们假设 II 型等温吸附中，多层吸附层为液化的吸附质，如液氮。接触角为 0 度。

通过 Young 氏方程，扩展压和真空润湿功的定义，我们可以得到：

表 1 列出了三个材料计算得到的真空润湿性和 BET 的 C 值。

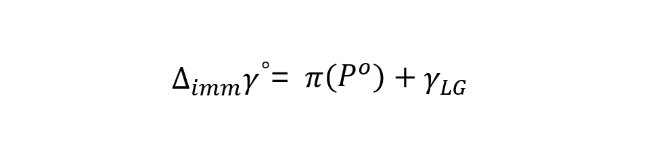
表 1 列出了三个材料计算得到的真空润湿性和 BET 的 C 值。

表1. 催化剂 A&B 以及负极碳材料 C 的真空液氮润湿功和 C 值

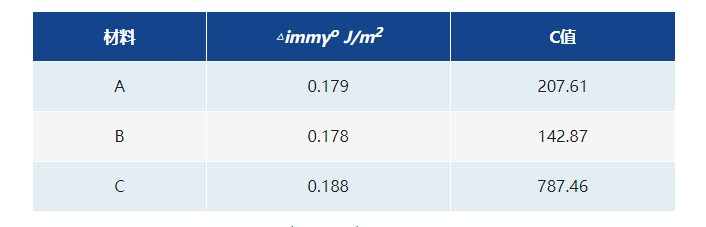
从表 1 可以看出，催化剂 A 和 B 的真空润湿功较为接近，其 C 值也接近。而负极 C 材料的润湿功最大，其 C 值也大很多。说明催化剂 A 和 B（皆为氧化铝负载金属催化剂）对液氮的润湿能力接近，但要弱于负极碳材料 C。BET 的 C 值也正是反映吸附质与吸附剂的作用力强弱，从中我们也可以看出，液化的吸附质的润湿能力与其气态相被吸附的能力呈正相关。

如果将吸附质换成其他气体或蒸汽，亦可以研究固体材料对各种其他润湿液体的真空可润湿性，对于工业生产和研发领域相当重要。Micromeritics 的 3Flex 三站全功能型多用气体分析仪就非常适合做各种气体和蒸汽吸附。

Micromeritics 3Flex 三站全功能型多用气体分析仪