 高级会员
高级会员
 已认证
已认证
BET
物理吸附过程中,在非常低的相对压力下,首先被覆盖的是高能量位。具有较高能量的吸附位包括微孔中的吸附位(因为其孔壁提供重叠的位能)和位于平面台阶的水平垂直缘上的吸附位(因有两个平面的原子对吸附质分子发生作用)。此外,在由多种原子组成的固体表面,吸附位能也会发生改变,这取决于暴露于表面的原子或官能团的性质。
但是,能量较高的位置首先被覆盖并不意味着随着相对压力增高、能量较低的位置不能被覆盖,而只是说明在能量较高的位置上物理吸附分子的平均停留时间较长。因此,当吸附质气体压力增高时,表面逐渐被覆盖,气体分子吸附于空白表面的几率增加。在表面被完全覆盖之前有可能形成第二吸附层或更多的吸附层。在实际情况下,不可能有正好覆盖单层的相对压力存在。BET理论可以在不管单分子层吸附是否形成的条件下,能有效地从实验数据获得形成单分子层所需的分子数目。
BET理论是Brunauer、Emmertt和Teller在1938年提出多层吸附模型,它发展了Langmuir单层吸附理论。他们把Langmuir动力学理论延伸至多层吸附,所作的假设除了吸附层不限于单层而可以是多层外,与Langmuir理论所作的假设完全相同。BET理论假设吸附在最上层的分子与吸附质气体或蒸气处于动力学平衡之中。
BET方程如下:
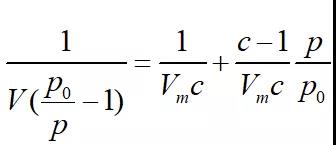
其中V——吸附气体体积;
Vm——单层吸附气体容量;
c——常数,与吸附剂、吸附质之间相互作用力有关;
p/p0——相对压力
利用实验数据,以1/[v(p0/p-1)]对p/p0作图,一般在相对压力0.05≤p/p0≤0.35间能得到一条很好的直线:
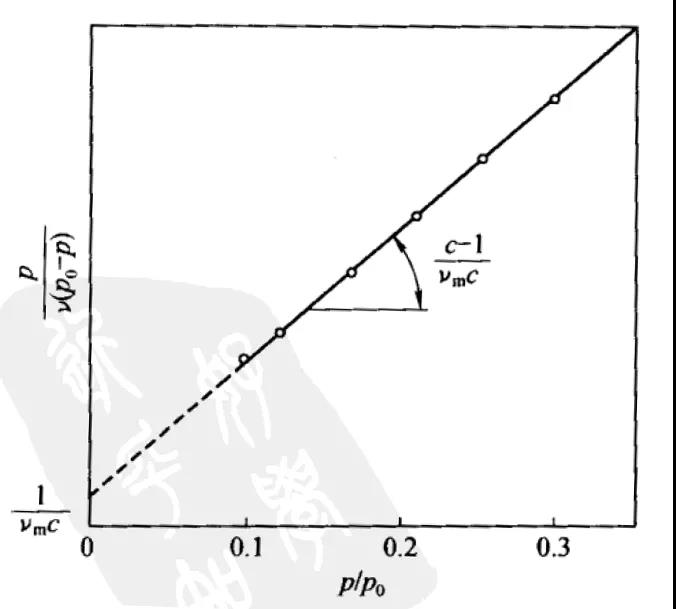
直线的拟合方程表示为:yA+Bx,截距A=1/Vmc,斜率B=(c-1)/Vmc。
从而可得:
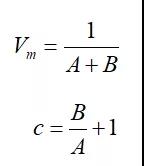
表面积 S=am·nm·NA
其中am——氮气在77K温度下液态六方密堆积的氮分子截面积,数值为16.2×10-20 m2;
nm——层吸附容量(mol),nm=Vm/22.414;
NA——Avogadro常数,数值为6.022×1023。
上述方程就是BET多点法计算比表面积的公式。



