Mie 散射系数的新算法

王少清 任中京　张希明　何芳 江海鹰

(山东建筑材料工业学院，济南　250022)

提要：介绍了一种计算Mie散射系数的新方法，给出了计算实例。

关键词：米氏散射，Mie系数，Mie计算

New algorithm of Mie scattering parameters

Wang Shaoqing  Ren Zhongjing　Zhang Ximing 　HeFang  Jiang Haiying

(Shandong Institute o f Building Materials，Jinan　250022)

Abstract：A new algorithm of calculating Mie Parameters was introduced. Some calculation results done with this algorithm were given.

Key words: Mie scattering ，Mie parameters，Mie calculation

1　引言

Mie 理论是球形颗粒对单色光的散射场分布的严格解析解^[1]，目前在环保、动力、气象、天文、两相流及粉体颗粒尺寸分布测量等工程技术领域中有广泛的应用。利用单一颗粒或颗粒群光散射场的测量数据。可以反推得散射颗粒或颗粒群的很多物理性质，如颗粒的尺寸、颗粒的折射率等^[2]。但反推必须事先计算出各种尺寸的颗粒在各种复折射率下的散射场分布数据。1968 年Dave^[3]最先发表了完整的Mie散射计算方法，以后Lentz^[4]和Wiscomb^[5]又针对部分计算提出了新算法。国内也有人发表了他们自己的算法^[6、7、8]。但总的看来，这些算法均有各自的局限性。尤其是当颗粒尺寸或折射率的虚部值较大时，往往计算速度过慢或产生溢出和不收敛等现象。本文介绍作者发展的Mie 散射新算法。该算法的特点是不受颗粒尺寸及折射率的限制，不会产生溢出和不收敛的现象，且具有较快的计算速度。

2　Mie散射系数的计算公式

Mie 散射计算的中心问题是计算Mie 散射系数a_n 和b_n，其表达式为^[9]

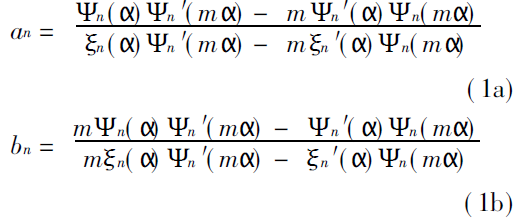
其中为颗粒的尺寸参数，定义为α=πd/λ，d为颗粒直径，λ为入射光在颗粒周围介质中的波长，而m为颗粒在周围介质中的相对复折射率，即m= m¹ + im² ( m²< 0) , 式中i 为虚数单位。而Ψ_n( Z) 和ξ_n( Z) ( Z 既表示α，又表示mα)的表达式为

Ψ_n( Z)=（πZ/2）J_n+1(Z)

ξ_n( Z)=Ψ_n( Z)+iΧ_n(Z)

Χ_n(Z)= ̶ (πZ/2)( ̶ 1)_n-1J_-(n-1)(Z)

     = ̶ (πZ/2)N_n+1(Z)

3 计算中产生溢出的原因

计算Mie 散射系数须先计算Ψ_n 和Χ_n。一般采用递推的方法。递推又分为向前递推( 即从n= 0 开始) 与向后递推( 即从n= N 开始至n=0, N 为预先设定值) 。实验表明，向前递推总是快于向后递推。Ψ_n 和Χ_n的初值为

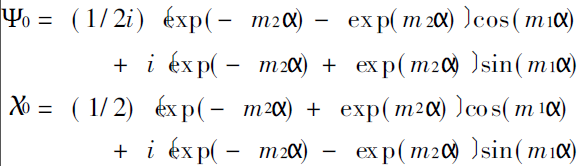
分析以上两式可知，当m₂≠0 时, 若颗粒尺寸d很大, 或复折射率的虚部值m₂很大，将使得乘积m₂d很大，可使两式中的项exp( - m₂ α) =exp ( - πm₂d/ λ) 的值超过计算机的数据限，从而产生溢出，这是产生溢出的重要原因。另外，在递推过程中，不恰当的算法也可能造成溢出。

4　a_n和b_n的新算法

为解决上述问题，作者提出了新的算法。将a_n和b_n的公式变形如下: 令

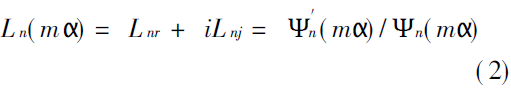
其中Lnr、Lnj分别表示Ln(m)的实部与虚部。将（2）式代入（1）式，并用a_nr、a_nj和b_nr、b_nj分别表示的实部与虚部。如此可推得

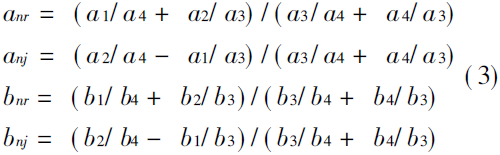
在上述四个公式中采用比值的形式是非常重要的，这样可避免递推过程中当a_i与b_i   较大时乘法运算可能产生的溢出。这是本算法的一个重要特点。在以上四式中

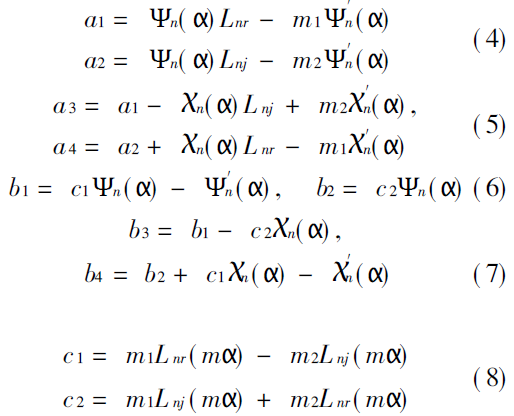
由于

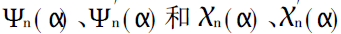
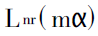
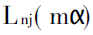
上面导出的(3) - (20)诸式，构成了Mie系数an和bn的完整算法。由于an和bn是从n= 1开始计算，利用初值公式(16) - (20)即可算得任意级数的an和bn的值，故没有舍入误差的问题。从(16)式可见，因为y= m₂ɑ≤0, 故无论m₂和ɑ取何值均不会产生溢出，再加上(3)的各式中采用了比的形式，又避免了计算过程中的溢出，这就从根本上解决了溢出的问题。

5　计算实例

利用以上算法编制了计算颗粒散射场强度和消光系数的计算机程序。当波长为λ的单位振幅的平面自然光入射颗粒时，颗粒的散射光强为^[9]

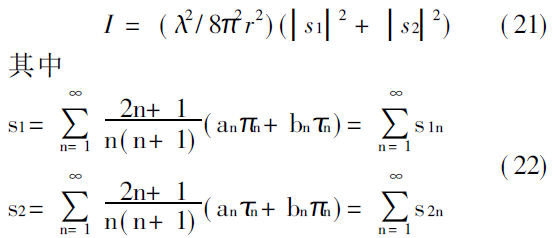
Ξ为计算机在双精度下的最小数据限。

图1示出散射光强的一组计算实例。其中取m₁=1.33，m₂=-0.4，λ=0.6328三图分别对应于颗粒的直径为d=0.001,1.0和30μm。而d图为颗粒直径d=100μm时散射花样的局部放大。可见，随着颗粒尺寸的增大，前向散射迅速加强，并且出现了复杂的旁瓣。

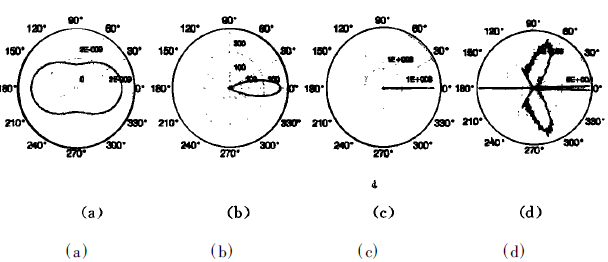
实部(a)与虚部(b)的变化情况。可见随着m₁和m₂的增大，虽然颗粒的尺寸保持不变，但散射也加强，且后向散射随着m₁和m₂的增大而加强。

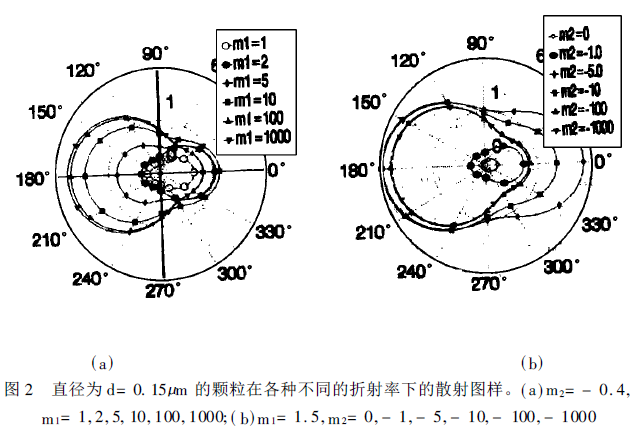
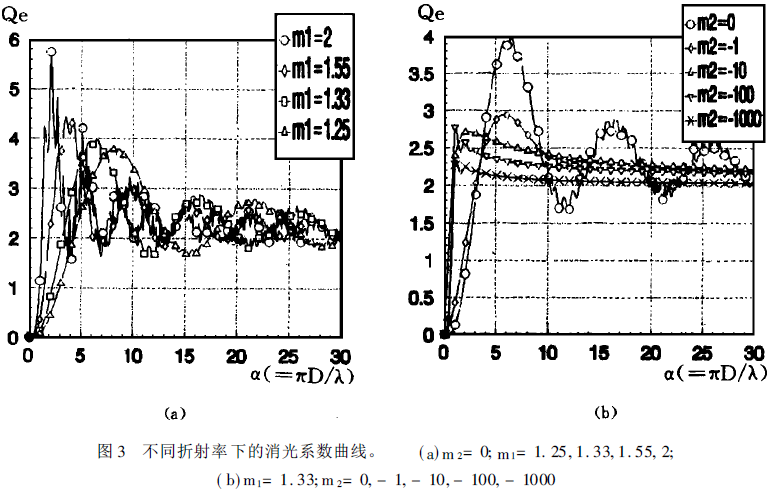
图3给出有关消光系数的计算结果，其中a)和b)分别表示消光系数随折射率实部与虚部的变化情况。可见随着颗粒直径的增大，消光系数趋近于2; 折射率的增大，尤其是折射率虚部的增大，使这一趋近变得更快和更明显。另外当折射率的虚部m₂= 0时，消光系数随颗粒直径的增大而振荡；但当m2≠0 时，振荡迅速消失。

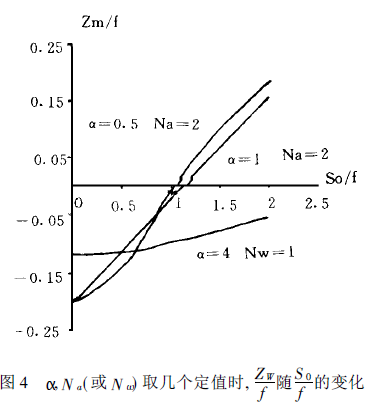
光强最大值处所对应的F_M(Z)的值即由上式确定。由上式也可见：此极限情况下的焦移大小主要由S₀/f及N_a所决定。

参考文献：

[1]M. Bor n and E. Wolf, Principles of optics ( sixt hedition ) , Pergaman Press ( OXFORD, NEW YORK, PARIS) , pp611(1980)

[2]Peter Chylek, V. Ramasw amy , A. Ashkin and J.M . Dziedzic,“Simultaneous determination o f refractiv endex and size o f spherical dielectric particles from light scattering data”,Appl. Opt . ,Vo l. 22, No . 15, p2302- 2307(1983)

[3]J. V. Dave, Repo rt 320 - 3237 ( IBM Scientific center , 1968)

[4]W. J. Lentz, Appl. Opt. , 15, 668( 1976)W. J. Wiscome, Appl. Opt, Vol. 19, No. 9, pp1505( 1980)

[6]顾冠亮等, 有关光散射物理量的数值计算, 上海机械学院学报, 1984 年4 期pp21

[7]余其铮等, Mie 散射算法的改进, 哈尔滨工业大学学报, 1987 年3 期, pp21

[8]郑刚等, M ie 散射的数值计算, 应用激光, Vol.12, No . 5, pp220( 1992)

[9]H. C. v an de Hulst , Lig ht scatter ing by small particles,Do ver Publica tion lnc. , New Yor k, chp. 13( 1981)