 白金会员
白金会员
 已认证
已认证
原理阐述
SSITKA 实验装置
SSITKA实验装置示意图如下图1所示,包含气路控制部分、反应器和质谱分析三部分[1]。气路控制部分要适合于稳态瞬变操作,保证迅速切换且前后状态处于稳定状态,同时质谱可以迅速响应。
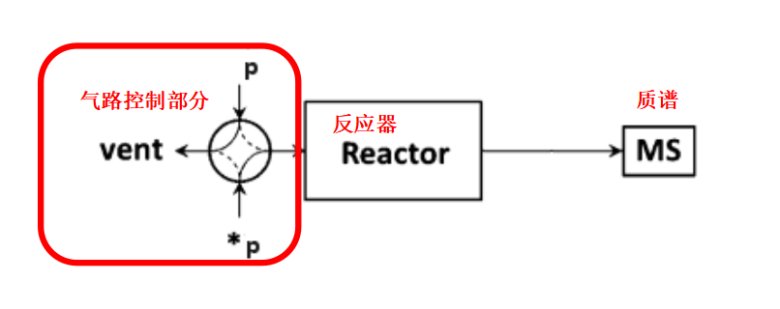
图1 SSITKA的实验装置示意图
当前大部分SSITKA实验是通过在微反上进行搭建而成,属于手动或者半自动装置,会带来手动误差。北京精微高博仪器有限公司的AMI 300TKA仪器通过特殊气路设置并配置质谱检测仪完成SSITKA实验,如下图2所示 AMI 300TKA软件界面图,气路控制部分由四通阀完成瞬变切换,Aux Gases和Blend Gases两种进料流分别通入未标记反应物12CO和同位素标记反应物13CO,四通阀切换后,反应物可由12CO转换为其同位素标记物13CO。
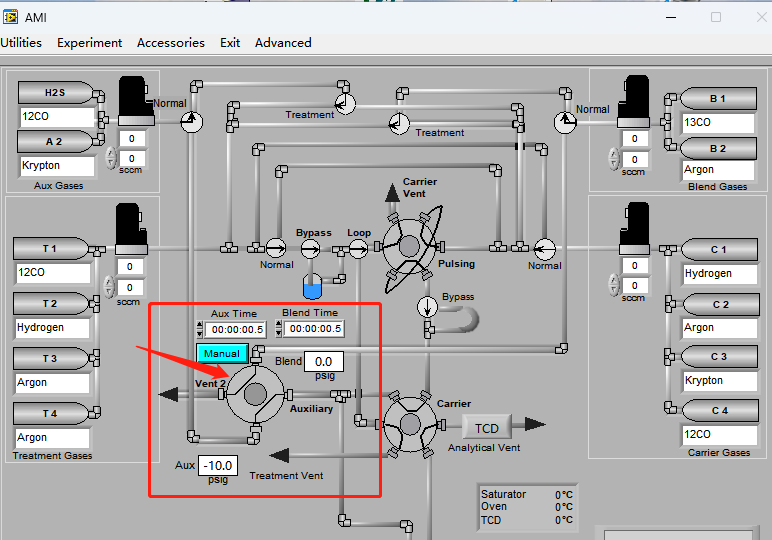
图2 AMI300TKA软件界面
SSITKA实验可通过下图3所示程序进行设置,完全自动,无需手动操作,方便可行,消除人为操作误差,保证测试结果的精确性。
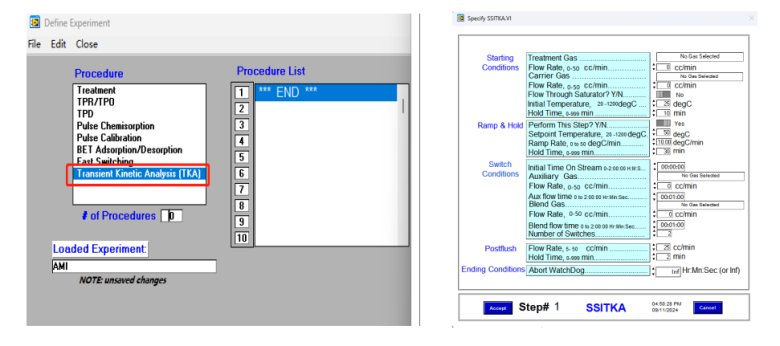
图3 AMI300TKA仪器SSITKA程序设置
SSITKA 动力学参数求解
一般参数求解
表面中间物种的表面停留时间 τP 和表面中间物种的量 NP
通过质谱检测到强度如下图4(a)所示,P为未标记产物,P*为其同位素标记产物,I是惰性示踪剂,t=0时刻四通阀切换,反应物转换为同位素标记物,产物P和惰性示踪剂I呈现衰减而同位素产物P*呈现递增响应,将产物P的衰减响应进行归一化处理得到瞬变响应曲线见下图4(b)。
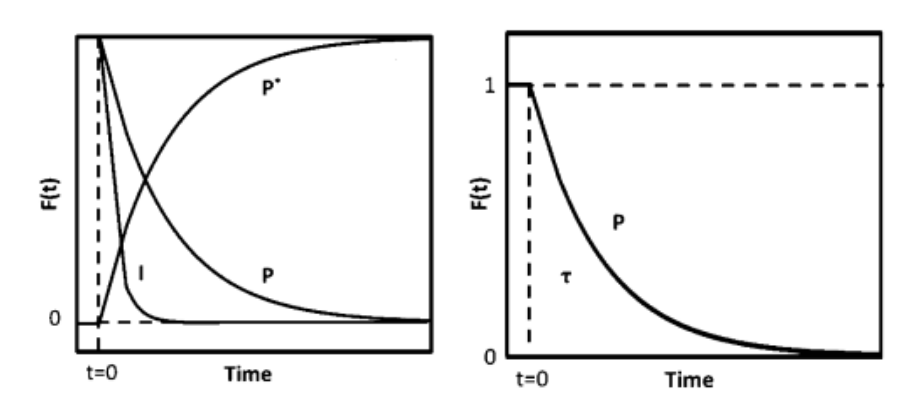
图4 (a)质谱图 (b)瞬变响应曲
不进行动力学假设、不建立表面机理模型,通过瞬变响应曲线可求取两个参数,生成产物P的中间物种表面停留时间(表面寿命) τP 和表面中间物种的量 NP ,NP 公式如下[2]:
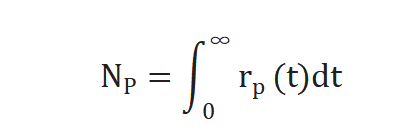
实验过程中对反应物进行快速切换,反应速率不变,未标记产物反应速率通过下列公式求得[3],r p(t)是未标记产物稳态反应速率,r p*(t) 和同位素标记产物的反应速率。
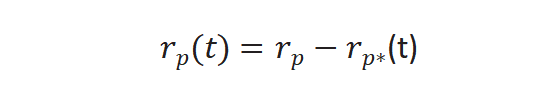
图4(b)所示未标记产物衰减归一化得到瞬变响应曲线,FP(t)公式如下:
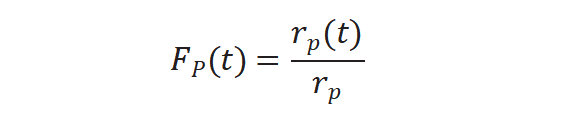
将上述三个公式重新排序计算得到中间物种的表面停留时间τP :
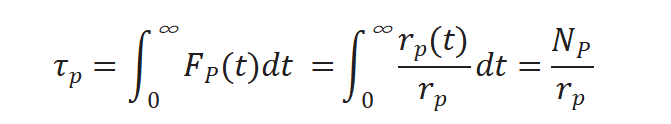
对瞬变响应曲线积分得出表面停留时间 τP,如图5所示。
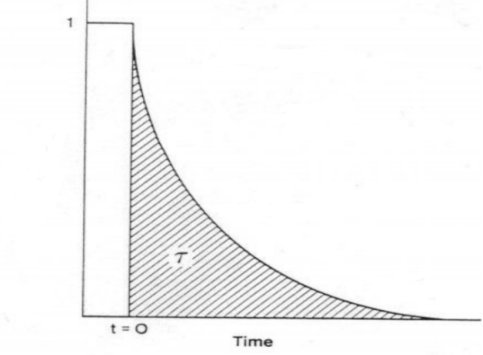
图5 表面停留时间 τP
表面中间物种覆盖度θ、反应速率常数K和周转频率TOF
采用化学吸附的方法测试出催化剂表面暴露的金属原子总数NC,通过表面中间物种的量NP计算出中间物种的表面覆盖度θ,公式如下:
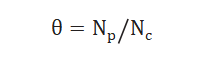
假设表面进行的化学反应为拟一级,拟一级反应的速率方程可表示为:
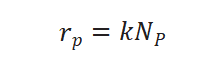
从而求得拟一级反应速率常数:
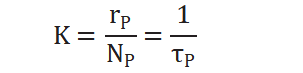
TOF周转频率表示单位时间内,单位活性位上发生催化反应的次数,这是基于表面活性位点数量的速率,是催化剂瞬时效率的量度,公式如下:
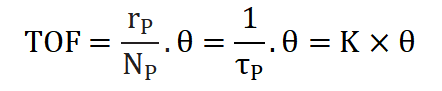
这里的为中间物种的表面覆盖率,通过反卷积技术可确定催化剂表面活性位点的数量和分布情况,可进一步研究催化反应动力学及其机理。
SSITKA 建模
一个非均相化学反应可能经历一个或多个催化剂表面中间步骤才能完成,而前面所求的一般参数表面中间物种的停留时间τP 和表面中间物种的量 NP 是生成产物 P 表面中间物种的总停留时间和表面中间物种的总量。为得到生成产物 P 的各中间物种的量及其寿命,Shannon [4]和 Chen [5]等在 Biloen[6]等工作的基础上,提出了下表1非均相反应催化剂表面机理模型,首先将反应分成可逆和不可逆两种情况,然后再进一步分成单一反应中间物种、串联反应中间物种、平行反应中间物种等几种情况,然后根据物料衡算,推导出瞬变响应模型,由瞬变响应模型求取各反应中间物种的量及其停留时间等动力学参数。

表1 由SSITKA获得的机理模型、瞬态响应和动力学参数
推断催化剂表面反应机理
Kobayashi [8]等通过实验发现通过分析响应曲线的形状,可以推断出反应机理。Shannon 等给出了单一反应中间物种、两个串联反应中间物种和两个平行反应中间物种的不可逆反应瞬间响应( 图6) 。
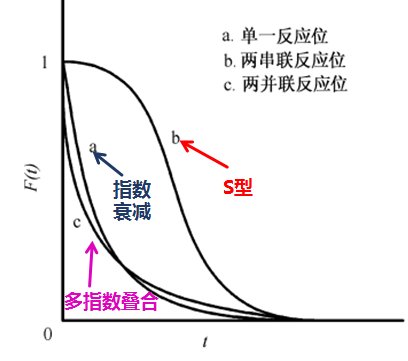
图6 不同表面反应机理的瞬变响应示意图
从上述图6中,瞬变响应曲线显示为 S 形,衰减最慢的曲线b为两串联反应位,这是由于两串联位顺序进行反应,用时较长;单指数衰减的瞬变响应曲线a为单一反应位;多指数衰减的瞬变响应曲线c为两并联反应位,这是因为并联反应位在各路径下平行反应,其衰减速率快呈现多指数叠合状。观察瞬变响应曲线可非常容易看出不同动力学模型的差异,从而推断出催化剂表面反应的差别。
SSITKA 实验中的影响因素
色谱效应和再吸附
反应物和产物不仅可以吸附在催化剂表面,也有可能吸附在反应器的管路和壁上而产生色谱效应,可通过缩短由四通阀到检测器的管路和反应器的长度,提高气体的流速,对管路采取保温措施来减小产生色谱效应的影响。AMI-300TKA采用1/16的管路减小死体积,对阀箱进行保温,MFC精确控制气体流速等措施提高测试精度。
SSITKA实验中产物的再吸附效应会对瞬变响应产生影响,若产物再吸附发生在活性位导致活性和反应速率下降,若产物再吸附发生在非反应活性位,虽活性不受影响,但测量的生成产物表面停留时间包括产物中间体真实停留时间和再吸附的停留时间。
上述情况一般采用加入惰性示踪剂和经验公式进行校正,修正公式如下:
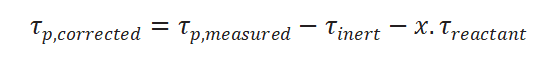
为惰性气体响应时的表面停留时间,此处x根据经验一般取0.5。
同位素效应
SSITKA 实验中假定反应处于稳态条件,忽略同位素效应,即假定同位素物种在动力学行为上没有差别,此时需特别注意氢及其同位素的使用,因为氢同位素间的质量和键能差别相对较大,由此会引起动力学和热力学上的差别。氢/氘(H/D)同位素交换时,动力学速率和表面中间物种可能产生较大变化,系统无法保持稳定状,因此采用H同位素实验时需注意。H/D同位素进行SSITKA实验可提供有关活性表面特征的信息,如H/D同位素交换实验能鉴别随着吸附、脱附或反应的进行,某一特定分子物种键的断裂。
SSITKA 与光谱的联用
SSITKA技术可以识别中间体的丰度及其动力学参数,其局限性是不能直接表征表面反应中间物的结构和直接监测其表面反应,而原位红外技术允许直接观察反应条件下的吸附物种[9]。将SSITK与FTIR有机地结合起来,可正确表征表面中间物种,包括其化学结构和表面覆盖度,并可分辨吸附反应物种和非反应物种[10]。下图7所示为北京精微高博仪器有限公司AMI-300TKA原位红外表征仪器,可以做原位表征。

图7 AMI-300TKA 原位表征
自20世纪70年代发明此项技术后它已经用于研究工业上许多不同和重要的化学反应机理。现今随着SSITKA与光谱技术的结合,可监测真实的表面中间体和反应机制。此外,SSITKA还可与其他方法如动力学建模、DFT等结合时,可以获得更多关于反应途径的信息。结合SSITKA和其他技术优势,在反应条件下获取尽可能多的信息,以阐明具有复杂化学反应的机理。
参考文献
[1]李春义 沈师孔 稳态同位素瞬变动力学分析 [J] 化学进展,1999,11(2):49-59.
[2]Recent Approaches in Mechanistic and Kinetic Studies of Catalytic, Cristian Ledesma,Jia Yang,De Chen, and Anders Holmen,ACS Catal. 2014, 4, 4527−4547
[3]Anders Holmen, Jia Yang, and De Chen Springer Handbook of Advanced Catalyst Characterization, Springer Handbooks,Part VII Transient and Thermal Methods,2023,41,935-966.
[4]Shannon, S. L.; Goodwin, J. G. Chem. Rev. 1995, 95, 677−695.
[5] Berger, R. J.; Kapteijn, F.; Moulijn, J. A.; Marin, G. B.; De Wilde,J.; Olea, M.; Chen, D.; Holmen, A.; Lietti, L.; Tronconi, E.;Schuurman, Y. Appl. Catal., A 2008, 342, 3−28.
[6]Kondratenko, E. V. Catal. Today 2010, 157, 16−23.
[7] Pansare, S.; Sirijaruphan, A.; Goodwin, J. G. In Isotopes in Heterogeneous Catalysis; Hutchings, G. J., Ed.; World Scientific Publishing Co.: London, 2006; Catalytic Science Series, Vol. 4, pp 183−206.[8]Kobayashi H,Kobayashi M ,Catal.Rev.-Sci.Eng.,1974,10,139.
[9]Yokomizo G H,Bell A T ,J .Catal.,1989,119,467—482.
[10] Efstathiou A M ,Chafik T ,Bianchi D et al.,J .Catal.,1994,148,224—239.



